How to manage materials

Introduction

Three types of materials are defined: fluid materials, solid materials, and thermal interface materials (TIM). A material can be assigned to a solid region, fluid region, or interface by selecting it from the material list or by defining a new one. The list of materials can be managed through the library page. This page contains a list of predefined materials, but you can define your materials as well. The predefined materials cannot be edited by anyone, your custom materials can.

All the predefined materials with constant properties are defined at Standard Temperature Pressure (STP) conditions. The STP conditions correspond to a temperature of 273.15 $K$ or 0$°C$ and a pressure of 100 $kPa$ or 1 $bar$. The properties of each type of material are given below:

Property		Material type
Name	Unit	Solid	Fluid	TIM
Density $\rho$	$kg/m^3$
Dynamic viscosity $\mu$	$kg/(m\cdot s)=Pa\cdot s$
Specific heat capacity $C_p$	$J/(kg\cdot K)$
Absorption coefficient $\alpha$	$m^{-1}$
Thermal conductivity $\kappa$	$W/(m\cdot K)$
Coefficient of thermal expansion $\beta$	$K^{-1}$
Thickness $R_d$	$m$
Resistivity	$\Omega \cdot m$
Thermal resistance $R_{th}$	$K/W$

Solids

Density

The density of a material is commonly denoted with the Greek letter rho $(\rho)$. The density can be set in three ways:

1. constant value at a reference temperature
2. a polynomial function of temperature where a maximum of 8 coefficients can be provided
3. table containing temperature and corresponding parameter value of the material at the specified temperature

Specific heat capacity

The specific heat capacity of a material is denoted as $C_p$. According to the thermodynamic models used, $C_p$ can be a constant or a temperature dependent value. In case of a constant, user specified values in $J/(kg\cdot K)$ are used. Otherwise, $C_p$ as a function of temperature is calculated using the available thermodynamic models. The specific heat capacity can be set in three ways:

1. constant value at a reference temperature
2. a polynomial function of temperature where a maximum of 8 coefficients can be provided
3. table containing temperature and corresponding parameter value of the material at the specified temperature

Thermal conductivity

The thermal conductivity of a material is denoted with the Greek letter kappa $(\kappa)$. The thermal conductivity of a material has the unit $W/(m\cdot K)$. It can be a constant provided by the user or can also be calculated using the transport coefficients from the transport model specified. An anisotropic conductivity can be defined by setting the appropriate thermal conductivity along the x-axis, y-axis, and z-axis. The thermal conductivity can be set in three ways:

1. constant value at a reference temperature
2. a polynomial function of temperature where a maximum of 8 coefficients can be provided
3. table containing temperature and corresponding parameter value of the material at the specified temperature

Absorption Coefficient

Thermal radiation models can be switched-on for certain types of simulations. For all boundaries, fluid or solid, the emissivity needs to be provided. Solid regions are considered to be participating in radiative heat transfer when radiation is turned on. Therefore, absorption coefficient $(\alpha)$ needs to be set for solid regions. Emissivity is a dimensionless number ranging between 0 and 1. Absorption coefficient has unit $m^{-1}$ and the value depends on the solid material.

Fluids

Density

The density of a material is commonly denoted with the Greek letter rho $(\rho)$. The density can be set in three ways:

1. constant value at a reference temperature
2. a polynomial function of temperature where a maximum of 8 coefficients can be provided
3. table containing temperature and corresponding parameter value of the material at the specified temperature

Dynamic viscosity

The dynamic viscosity of a material is commonly denoted with the Greek letter mu $(\mu)$. It is important to note that we use dynamic viscosity with unit $Pa\cdot s$ and not the kinematic viscosity. Viscosity should only be defined for fluids. The dynamic viscosity can be set in three ways:

1. constant value at a reference temperature
2. a polynomial function of temperature where a maximum of 8 coefficients can be provided
3. table containing temperature and corresponding parameter value of the material at the specified temperature

Specific heat capacity

The specific heat capacity of a material is denoted as $C_p$. According to the thermodynamic models used, $C_p$ can be a constant or a temperature dependent value. In case of a constant, user specified values in $J/(kg\cdot K)$ are used. Otherwise, $C_p$ as a function of temperature is calculated using the available thermodynamic models. The specific heat capacity can be set in three ways:

1. constant value at a reference temperature
2. a polynomial function of temperature where a maximum of 8 coefficients can be provided
3. table containing temperature and corresponding parameter value of the material at the specified temperature

Thermal conductivity

The thermal conductivity of a material is denoted with the Greek letter kappa $(\kappa)$. The thermal conductivity of a material has the unit $W/(m\cdot K)$. It can be a constant provided by the user or can also be calculated using the transport coefficients from the transport model specified. An anisotropic conductivity can not be defined for fluids. The thermal conductivity can be set in three ways:

1. constant value at a reference temperature
2. a polynomial function of temperature where a maximum of 8 coefficients can be provided
3. table containing temperature and corresponding parameter value of the material at the specified temperature

Coefficient of thermal expansion

Materials change shape, area, or volume depending on the temperature change. Coefficient of thermal expansion denoted as beta $(\beta)$ is used to quantify this behavior. The unit for thermal expansion coefficient is $K^{-1}$. The thermal expansion coefficient can be set in three ways:

1. constant value at a reference temperature
2. a polynomial function of temperature where a maximum of 8 coefficients can be provided
3. table containing temperature and corresponding parameter value of the material at the specified temperature

Thermal interface materials (TIM)

The thermal interface is commonly used in thermal management applications to facilitate effective thermal path between components. Examples of thermal interface materials are thermal greases, thermal tapes, etc. Thermal interface materials are defined by two properties - thermal conductivity and the thickness of the interface. The thermal conductivity $\kappa$ is specified in $W/(m\cdot K)$ and the thickness $R_d$ in meters $m$. ColdStream also allows to input the thermal resistivity $R_{th}$ in $W/K$.

How to input temperature-dependent material properties?

For fluids, it is possible to enter temperature-dependent values. The following input options are possible:

1. A constant value at a reference temperature:
   $\kappa = 100$
2. A polynomial in function of temperature where a maximum of 8 coefficients can be provided:
   $\kappa = [1,2,3,4,5,6,7,8]$
   This array represents the coefficients of a polynomial:
   $\kappa = 1+2T+3T^2+4T^3+5T^4+6T^5+7T^6+8T^7$
3. A table containing the temperature and corresponding parameter value of the material at the specified temperature:
   $\kappa = [[273,100],[283,100],[293,120],[303,120]]$

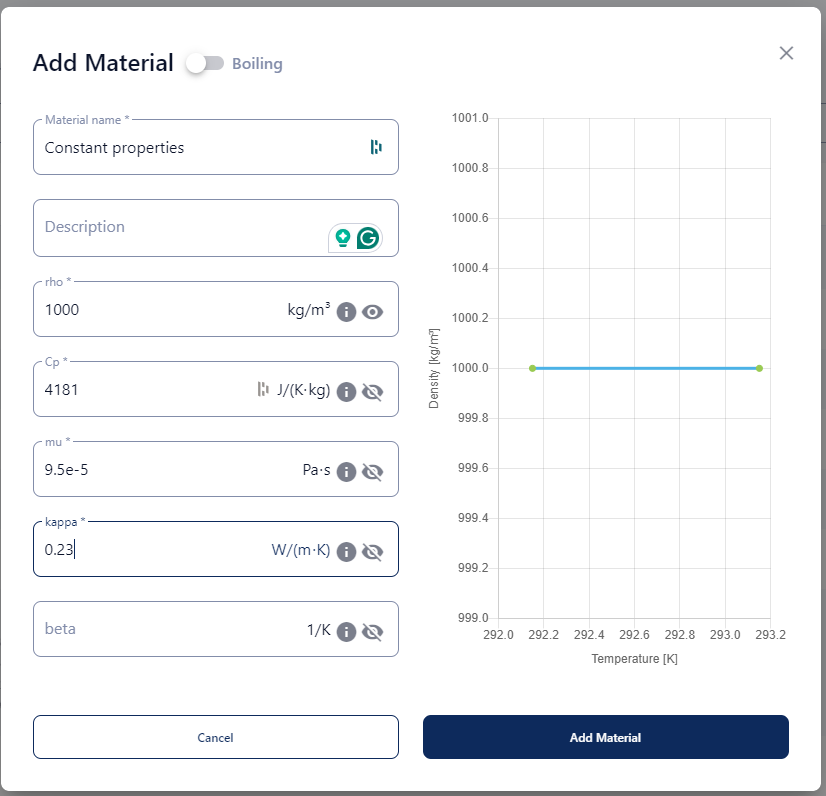
Example of a constant input

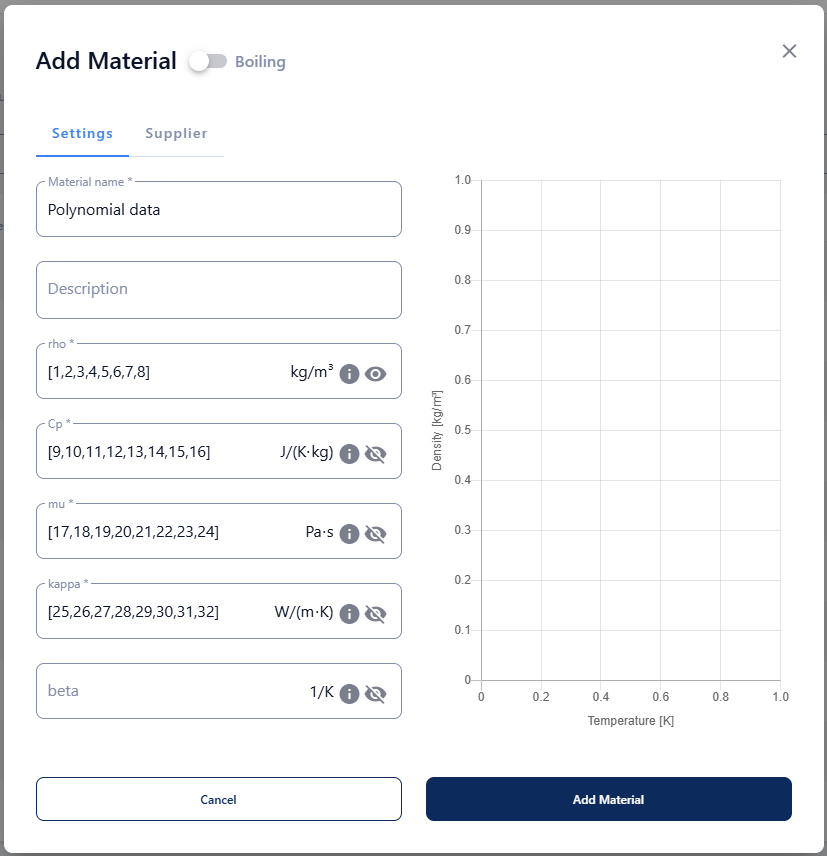
Example of a polynomial input for kappa

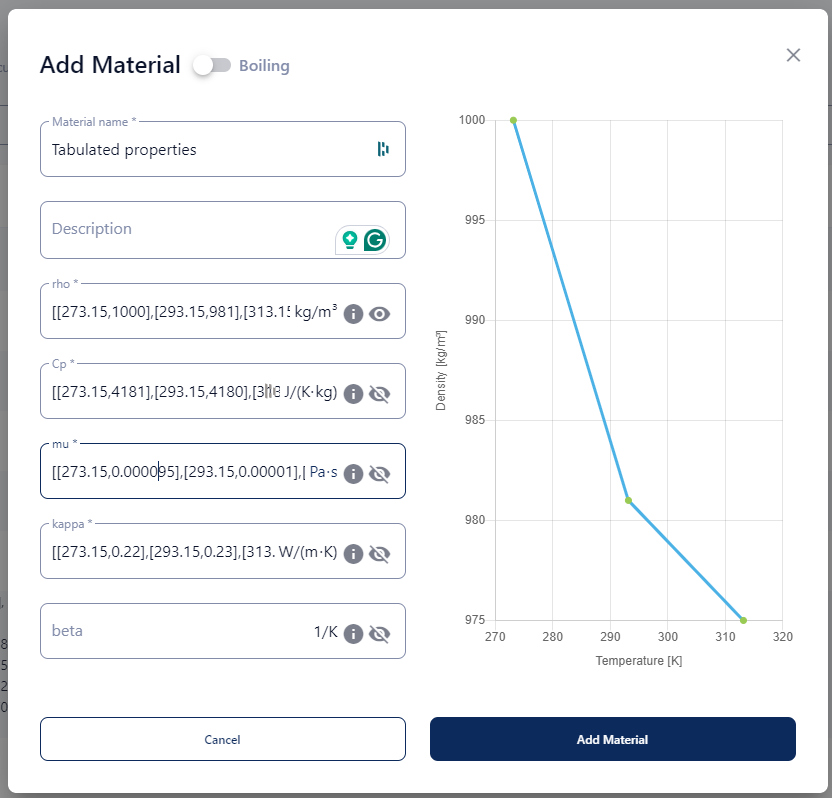
Example of a tabulated input for kappa

📘

Note

It is not possible to insert temperature-dependent properties for solids or thermal interfaces, only for fluids.

❗️

Important

When creating a fluid, the input for all properties should be identical. This means that either all properties are constant, or tabulated or polynomial, mixing them is not accepted.